Theory

A Full Wave Rectifier is a circuit, which converts an ac voltage into a pulsating dc voltage using both half cycles of the applied ac voltage. It uses two diodes of which one conducts during one half cycle while the other conducts during the other half cycle of the applied ac voltage.

During the positive half cycle of the input voltage, diode D1 becomes forward biased and D2 becomes reverse biased.Hence D1 conducts and D2 remains OFF. The load current flows through D1 and the voltage drop across RL will be equal to the input voltage.

During the negative half cycle of the input voltage, diode D1 becomes reverse biased and D2 becomes forward biased.Hence D1 remains OFF and D2 conducts. The load current flows through D2 and the voltage drop across RL will be equal to the input voltage.

Ripple Factor

The ripple factor for a Full Wave Rectifier is given by

  

The average voltage or the dc voltage available across the load resistance is

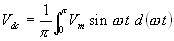
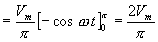
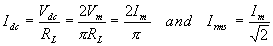
RMS value of the voltage at the load resistance is

Efficiency

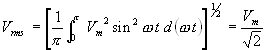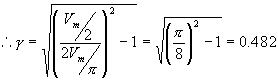Efficiency, h is the ratio of dc output power to ac input power

The maximum efficiency of a Full Wave Rectifier is 81.2%.

Transformer Utilization Factor

Transformer Utilization Factor, TUF can be used to determine the rating of a transformer secondary. It is determined by considering the primary and the secondary winding separately and it gives a value of 0.693.

Form Factor

Form factor is defined as the ratio of the rms value of the output voltage to the average value of the output voltage.

Peak Factor

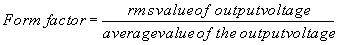
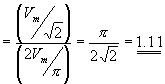
Peak factor is defined as the ratio of the peak value of the output voltage to the rms value of the output voltage.

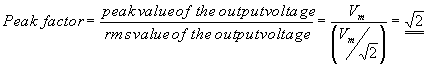
  Peak inverse voltage for Full Wave Rectifier is 2V_m because the entire secondary voltage appears across the non-conducting diode. This concludes the explanation of the various factors associated with Full Wave Rectifier.

Rectifier with Filter

   The output of the Full Wave Rectifier contains both ac and dc components. A majority of the applications, which cannot tolerate a high value ripple, necessitates further processing of the rectified output. The undesirable ac components i.e. the ripple, can be minimized using filters.

 

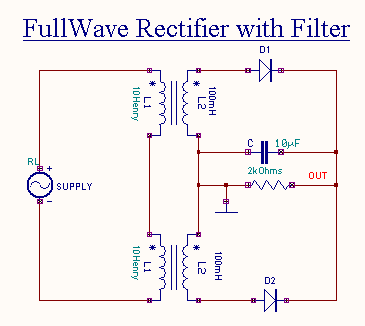
 The output of the rectifier is fed as input to the filter. The output of the filter is not a perfect dc, but it also contains small ac components.

  Some important filters are

1. Inductor Filter
2. Capacitor Filter
3. LC Filter
4. CLC or p Filter

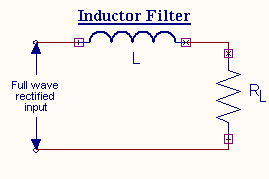
 Inductor Filter

The figure shows an inductor filter.When the output of the rectifier passes through an inductor, it blocks the ac component and allows only the dc component to reach the load.

Ripple factor of the inductor filter is given by .

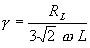   The above equation shows that ripple will decrease when L is increased and R_L is decreased. Thus the inductor filter is more effective only when the load current is high (small R_L). The larger value of the inductor can reduce the ripple and at the same time the output dc voltage will be lowered as the inductor has a higher dc resistance.

    The operation of the inductor filter depends on its property to oppose any change of current passing through it. To analyze this filter for full wave,

the Fourier series can be written as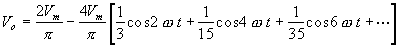

The dc component is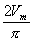

    Assuming the third and higher terms contribute little output, the output voltage is

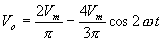
   The diode, choke and transformer resistances can be neglected since they are very small compared with R_L. Therefore the dc component of current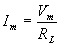

   The impedance of series combination of L and R_L at 2w is

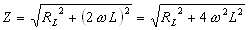
   Therefore for the ac component,

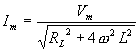
   Therefore, the resulting current i is given by,

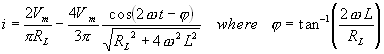
   The ripple factor which can be defined as the ratio of the rms value of the ripple to the dc value of the wave, is

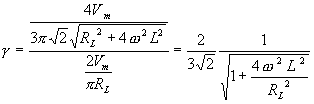
If 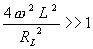, then a simplified expression for g is

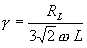
   In case, the load resistance is infinity i.e., the output is an open circuit, then the ripple factor is 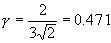. This is slightly less than the value of 0.482. The difference being attributable to the omission of higher harmonics as mentioned. It is clear that the inductor filter should only be used where R_L is consistently small.

Capacitor Filter

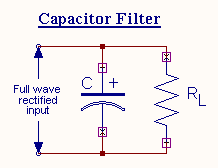
   A capacitor filter connected directly across the load is shown above. The property of a capacitor is that it allows ac component and blocks dc component. The operation of the capacitor filter is to short the ripple to ground but leave the dc to appear at output when it is connected across  the pulsating dc voltage.

   During the positive half cycle, the capacitor charges upto the peak vale of the transformer secondary voltage, V_m and will try to maintain this value as the full wave input drops to zero. Capacitor will discharge through R_L slowly until the transformer secondary voltage again increase to a value greater than the capacitor voltage. The diode conducts for a period, which depends on the capacitor voltage. The diode will conduct when the transformer secondary voltage becomes more than the diode voltage. This is called the cut in voltage. The diode stops conducting when the transformer voltage becomes less than the diode voltage. This is called cut out voltage.

   Referring to the figure below, with slight approximation the ripple voltage can be assumed as triangular. From the cut-in point to the cut-out point, whatever charge the capacitor acquires is equal to the charge the capacitor has lost during the period of non-conduction, i.e., from cut-out point to the next cut-in point.

The charge it has acquired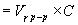

The charge it has lost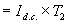

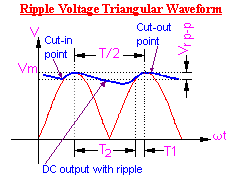
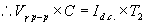
    If the value of the capacitor is fairly large, or the value of the load resistance is very large, then it can be assumed that the time T₂ is equal to half the periodic time of the waveform.

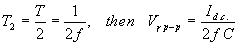
    From the above assumptions, the ripple waveform will be triangular and its rms value is given by

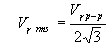
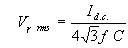
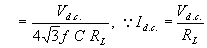
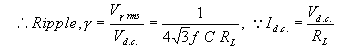
   The ripple may be decreased by increasing C or R_L (both) with a resulting increase in the dc. output voltage.

LC Filter

The ripple factor is directly proportional to the load resistance R_L in the inductor filter and inversely proportional to R_L in the capacitor filter. Therefore if these two filters are combined as LC filter or L section filter as shown in figure the ripple factor will be independent of R_L.

 

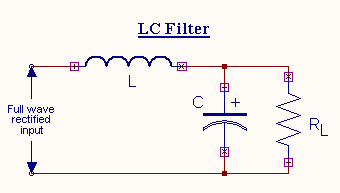
   If the value of inductance is increased it will increase the time of conduction. At some critical value of inductance, one diode, either D1 or D2 will always conducting.

   From Fourier series, the output voltage can be expressed as

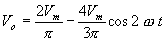
The dc output voltage,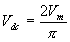

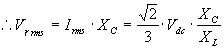
The ripple factor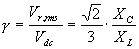

 

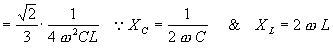
CLC or p Filter

 

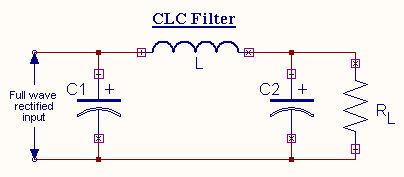
   The above figure shows CLC or p type filter, which basically consists of a capacitor filter, followed by LC section. This filter offers a fairly smooth output and is characterized by highly peaked diode currents and poor regulation. As in L section filter the analysis is obtained as follows.

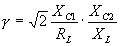
   Procedure

   EDWinXP-> Schematic Editor: The circuit diagram is drawn by loading components from the library. Wiring and proper net assignment has been made. The values are assigned for relevant components.

 

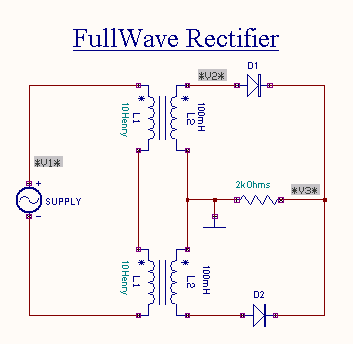
  EDWinXP -> Mixed Mode Simulator: The circuit is preprocessed. The test points and waveform markers are placed in input and output of the circuit. GND net is set as reference net. The Transient Analysis parameters have been set. The Transient Analysis is executed and output waveform is observed in Waveform Viewer.

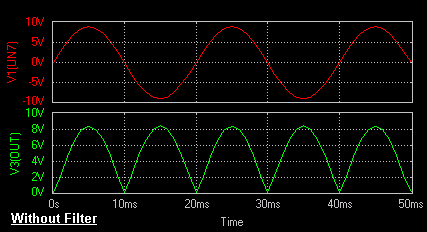
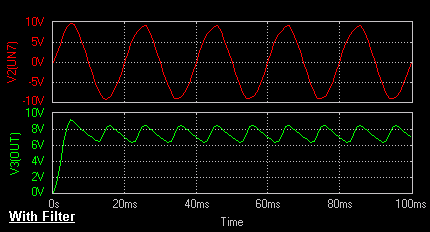
  Result

   The output waveform for Full Wave Rectifier with filter and without filter may be observed in the waveform viewer.